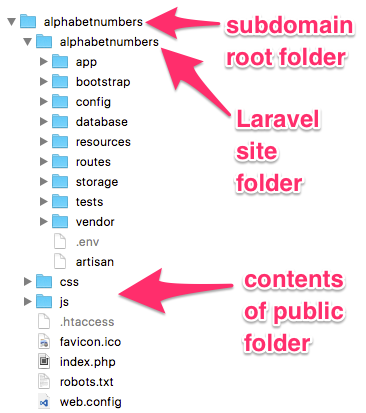
Running Laravel 5 on a shared host subdomain (I use Vidahost) is a little daunting because Laravel requires the web root to point to the /public folder and generally with a subdomain the website root is the root folder that is created for you.
My solution was to create a directory in the subdomain root folder and copy all the code into there. I then copied the contents of the /public folder into the subdomain root folder and edited index.php.
The two require lines need modifying to remove the ‘..’ characters and replace with the actual path.
//require __DIR__.'/../bootstrap/autoload.php';
require __DIR__.'/mysubdirectory/bootstrap/autoload.php';
It’s not pretty but it worked OK.
The little application I wrote is to help with non-verbal reasoning tests, to memorise the numeric equivalents of the alphabet: Alphabet to Numbers.
Isn’t it better to avoid shared hosting? Since it has serious drawbacks regarding security and performance, a VPS, like DigitalOcean, is a better option. If a person doesn’t have sysadmin skill to start a DO droplet, then they can instead use managed platform, like Cloudways, to setup Laravel on DO server.
What about editing .htaccess file in root folder instate of coping the content of the public folder?
in fact we redirect users to laravel’s public folder with htaccess in root folder and do anything else with laravel’s htaccess file located in public folder.
hah? This works for me but is this have a wrong way?
which is better ? what’s the benefit of your code ?